Crystal growth remains a very important area in the field of Materials Science. The semiconductor and optoelectronic materials industries are placing ever increasing demands on the variety of processes used to produce crystalline materials. The exacting requirements placed on processing techniques is epitomized by the current efforts in nanostructured materials.
The minimization or elimination of defects in crystal growth is one of the primary objectives of mathematical modeling of processing techniques. The very successful collaboration between individuals in ACMD and the Metallurgy Division in MSEL continues (this work is partially supported by NASA). The researchers in ACMD contribute to the models with both solution methodologies and physical insight to the fundamental processes. This effort has resulted in the development of predictive models for a variety of crystal growth techniques from the liquid phase. These models consist of both analytic relations under restrictive simplifications and very sophisticated numerical algorithms to treat the nonlinear behavior under more general conditions. The recent focus of this modeling research addresses the specific concerns associated with crystals that grow with faceted or stepped interfaces at very small length scales. This situation occurs for materials which have high anisotropy (preferred orientations) in either their surface energy or atomic attachment kinetics.
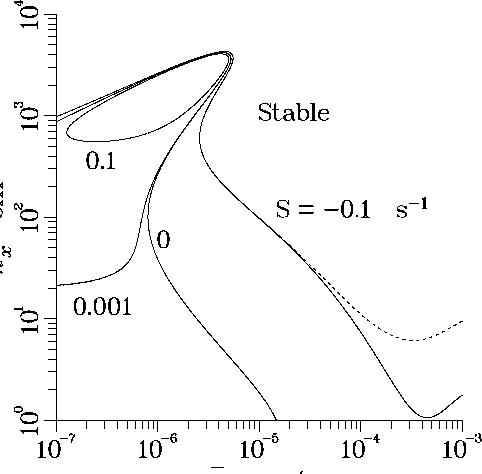
The current phase of this research has been to investigate the effect of fluid flow on the interface structure (morphology) in stepped growth from a supersaturated solution. A shear flow along the interface, either imposed or resulting from natural convection, has been found experimentally to impact the morphology of the growing interface and, consequently, the formation of defects. The fluid flow can interact strongly with the step motion and cause decreased stability for a flow in the same direction as the step motion and enhanced stability for flows counter to step motion. As an example of the quantitative predictions resulting from this modeling work, the following figure is a stability diagram which yields critical values for the size of an interface disturbance as a function of the interface growth velocity.

Caption:
The ordinate is a measure of the spatial scale of an interface disturbance (spatial wavenumber, 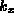 ) which is plotted versus the interface velocity
for growth from solution. The curves represent the stability/instability
demarcation for various values of the shear rate, S, resulting from
the fluid flow.
) which is plotted versus the interface velocity
for growth from solution. The curves represent the stability/instability
demarcation for various values of the shear rate, S, resulting from
the fluid flow.
The various curves pertain to different shear rates (S) resulting from the fluid flow. Positive S values lead to a stabilization while negative values cause a destabilization, which is readily seen by comparing to the no flow (S=0) case. The particular results shown are based on parameter values that represent an inorganic compound used as a nonlinear optical material.
Two significant accomplishments have been to quantify flow-interface interactions for a range of processing conditions for solution growth and for directional solidification of a binary alloy. The next stage of the project is to model the effect of oscillating the shear flow at the growing interface to determine whether this type of temporal modulation can be used to control the stability of the growing interface structure.