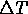Geoffrey B. McFadden ACMD
Sam R. Coriell, Materials Science and Engineering Laboratory
Robert F. Sekerka, Carnegie Mellon University
An outstanding problem in solidification theory is to predict the length scales and time scales that occur during crystal growth. These scales are crucial in determining the physical properties of the solidified material; for example, when multicomponent alloys are produced by directional solidification, instabilities of the solid-liquid interface can lead to inhomogeneous solute patterns, or microsegregation, in the solid phase which are generally undesirable. Predicting the conditions under which microsegregation occurs, and the associated length scales, is therefore a problem that receives much attention both experimentally and theoretically.
Recently M.E. Glicksman, of the Rensselaer Polytechnic Institute, and colleagues have performed fundamental studies of growth of a single-component material from a supercooled melt. When the liquid phase is maintained at temperatures below the equilibrium melting point of the material, the solid that forms spontaneously has a dendritic, or branch-like structure, with primary stems growing at constant velocity into the melt. The tip velocities, the radius of curvature of the tip, and other features of the dendrites are fundamental properties that Glicksman et al. are able to measure experimentally, and are used to critically assess various theoretical predictions for these quantities.
An experimental complication is the occurrence of natural convection
in the liquid phase, which is driven by buoyancy forces produced by
the density variations associated with the temperature gradients in the system.
The effect of the convection is to alter the transport of heat away from
the solidifying dendrite, so that the resulting tip velocity and
radius of curvature of the tip are modified.
In order to reduce the effects of this buoyancy-driven convection,
the experiments have been performed in a reduced gravity environment
on board the NASA space shuttle. Examination of typical data for both
terrestrial growth conditions and the microgravity conditions of space
show that in both cases there are significant effects that may be attributed
to natural convection; an example is shown in the accompanying figure.
Here the tip velocity, V, is plotted as a function of
the amount of thermal undercooling,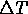 
, of the liquid below the
bulk melting point of the material. Data is shown for both
terrestrial conditions (circles) and for microgravity conditions (squares).
If convection effects were absent, the experimental data would be expected to fall on the bottom-most curve shown in the figure, which represents a theoretical prediction based on a model that includes no convective effects. Both sets of data show good agreement with the model at large velocities and large undercoolings, but show systematic deviation from the predicted behavior at smaller velocities. The agreement is better for the microgravity data (squares), which can be attributed to the decreased importance of buoyancy because of the reduced gravity. Both sets of data eventually deviate from the bottom curve at low enough undercoolings, implying that even under microgravity conditions natural convection can play a significant role.
To help understand the observed behavior, we have developed a simple model that takes into account effects of buoyancy-driven convection. The model assumes that because of natural convection the fluid is well-mixed and isothermal outside of a boundary layer or stagnant film near the surface of the dendrite, and assumes that the heat transport within the stagnant film takes place by diffusion alone. A closed-form solution to the thermal problem can be found that depends on the assumed thickness of the stagnant film. The macroscopic flow outside the stagnant film is given by a large Raleigh number approximate solution in which the region consisting of the network of growing dendrites is approximated by an isothermal sphere of radius R. The stagnant film thickness is then determined self-consistently by a balance of convective and diffusive heat transfer at the edge of the stagnant film.
The predictions of the resulting theory are shown as the top curves
in the figure. The theory depends on a single adjustable parameter,
representing the ratio of the gravitational acceleration, g, and the radius, R.
The top three curves in the figure correspond to the terrestrial value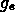 
for g and radii of 
, 
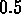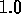, and 
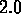cm, which are
typical of the geometries in the experiments. The bottom three curves
correspond to R = 1 cm and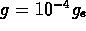 
, 
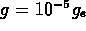, and
g = 0. The theory does a good job of
predicting the values of undercooling for which the effects of convection
become important.
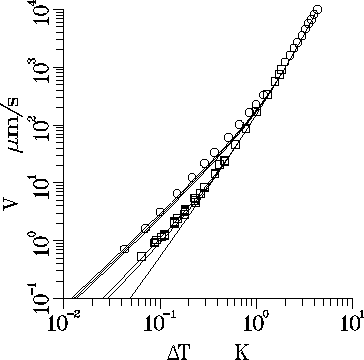
Figure 4: Comparisons of experimental data of Glicksman et al. for the
dendrite tip velocity V as a function of thermal undercooling
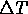with predictions of a simple model that includes the effects
of natural convection. The circles correspond to terrestrial growth
conditions, and the squares correspond to microgravity growth conditions.