Matrix Market

[ Home ] [ Search ] [ Browse ] [ Resources ]

Spectral Portraits

This page was kindly contributed to the Matrix Market by Alan McCoy, Vincent Toumazou, and Valerie Fraysse of the Qualitative Computing Group at CERFACS.

Example 1 Example 2 Example 3 Example 4

Contents

What is a spectral portrait ?

Eigenvalues of nonsymmetric matrices play an essential role in physical problems. These eigenvalues may be used either for their physical meaning (vibration modes, stability region, etc.) or for their numerical meaning (convergence of numerical scheme, etc.). Perturbations on the computed eigenvalues are the consequence of perturbations E on the matrix A. These perturbations may come from physics (uncertainty on the data, etc.) and/or from numerics (numerical approximations, finite precision arithmetic). The spectral portrait is a graphical tool that provides the user with information about the spectral sensitivity of the spectrum of a matrix. It gives a visualization of the $\epsilion$-pseudospectrum which is the set defined by

$\Gamma_\epsilon = { z \in C; z is an eigenvalue of A+E with ||E||_2 \leq \epsilion ||A||_2}$.

Equivalently, $\Gamma_\epsilon = { z \in C; ||(A-zI)^{-1}||_2 ||A||_2 \ge \epsilon^{-1}$. The spectral portrait consists in the representation of

$z \rightarrow spp(z) = \log_10 ||(A-zI)^{-1}||_2 ||A||_2$.

in the complex plane.

Back to top of page

How to read a spectral portrait

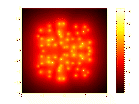
Let A be the companion matrix of order 10 associated with the monic polynomial $p(x) = (x-1)^3 (x-2)^3 (x-3)^3 (x-4) = x^{10} + \sun_{i=0}^9 a_i x^i$. The matrix A is called the ``Rose'' matrix.

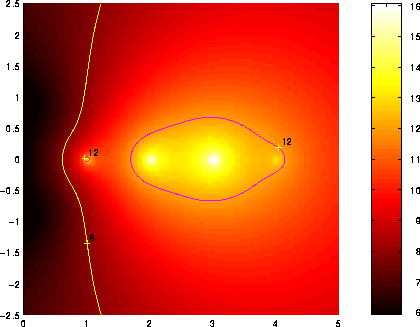
Spectral portrait of the ``Rose'' matrix
Figure 1.1: Spectral portrait of the ``Rose'' matrix

Figure 1.1 gives the spectral portrait of A. The choice of colours and scale permits to see easily the contours of the $\epsilon$-pseudospectrum for values of $\epsilon$ from $10^{-6}$ to $10^{-16}$. We have added the contour lines corresponding to $\epsilon = 10^{-8}$ and to $\epsilon = 10^{-12}$. Consider the region enclosed inside the border associated with $\epsilon = 10^{-12}$ : this region is the set of all eigenvalues of all the matrices (A+E) for $||E|| \le 10^{-12} ||A||$. Another interpretation is the following. Suppose that the matrix A is known to the normwise relative precision $10^{-8}$ for instance. Then, the region enclosed inside the border associated with $\epsilon = 10^{-8}$ is the set of all possible eigenvalues for this matrix. In particular, if one tries to compute the eigenvalues of A in single precision with a stable algorithm, one might get any of the points contained in this 10^{-8}-pseudospectrum. In our case, this region is very large because the matrix A is a highly nonnormal matrix with defective eigenvalues.

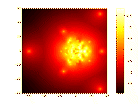
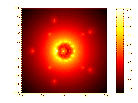
An example from the Harwell-Boeing collection Figure 1.2 (resp., 1.3) shows the spectral portrait of the Tolosa matrix of size n = 5000 (resp., n = 10000). All the eigenvalues of Tolosa are simple but the eigenvalues of largest imaginary part are the most unstable. They are the ones of interest to engineers.

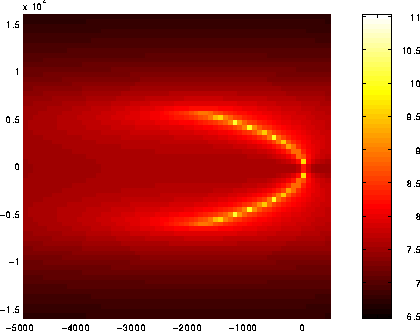
Spectral portrait for Tolosa5000
Figure 1.2: Spectral portrait for Tolosa5000

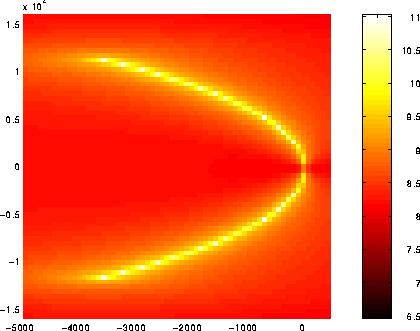
Spectral portrait for Tolosa10000
Figure 1.3: Spectral portrait for Tolosa10000

Back to top of page

More on spectral portraits

Back to top of page

The Matrix Market is a service of the Mathematical and Computational Sciences Division / Information Technology Laboratory / National Institute of Standards and Technology

[ Home ] [ Search ] [ Browse ] [ Resources ]

Last change in this page : 26 August 2003. [ ].