Matrix Set QCD

QCD: Quantum Chromodynamics

from the Independent Sets and Generators

Set QCD
Source:	Bjoern Medeke, Department of Mathematics, Institute of Applied Computer Science, University of Wuppertal, 42097 Wuppertal, Germany. Phone: +49 202 439-3776. Email: [email protected]
Discipline:	Physics
Accession:	December 2000

Background. Lattice gauge theory is a discretization of quantum chromodynamics which is generally accepted to be the fundamental physical theory of strong interactions among the quarks as constituents of matter. The most time-consuming part of a numerical simulation in lattice gauge theory with Wilson fermions on the lattice is the computation of quark propagators within a chromodynamic background gauge field. These computations use up a major part of the world's high performance computing power.

Quark propagators are obtained by solving the inhomogeneous lattice Dirac equation Ax = b, where A = I - kD with 0 <= k < k_c is a large but sparse complex non-Hermitian matrix representing a periodic nearest-neighbour coupling on a four-dimensional Euclidean space-time lattice.

From the physical theory it is clear that the matrix A should be positive real (all eigenvalues lie in the right half plane) for 0 <= k < k_c. Here, k_c represents a critical parameter which depends on the given matrix D. Denoting

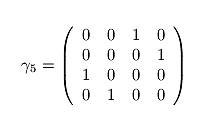
$\gamma_5 = \left( \begin{array}{cccc}0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \end{array}\right)$ the Wilson fermion matrix A is Gamma-5 symmetric,

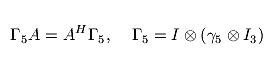
$\Gamma_5 A = A^H \Gamma_5,\;\;\;\;\Gamma_5 = I \otimes ( \gamma_5 \otimes I_3 )$

Due to the nearest neighbour coupling, the matrix A has 'property A'. This means that with a red-black (or odd-even) ordering of the grid points the matrix becomes

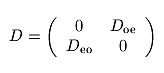
A = I - kD with $D = \left( \begin{array}{cc}0 & D_{\rm oe} \\D_{\rm eo} & 0 \end{array}\right)$

Set of QCD Matrices. The QCD matrices provided in the set QCD consist of realistic matrices D generated at different physical temperatures b.

matrix D	b	order	nonzeros	*k_c*
`conf5.0-00l4x4-1000.mtx`	5.0	3072	119808	0.20611
`conf5.0-00l4x4-1400.mtx`	5.0	3072	119808	0.20328
`conf5.0-00l4x4-1800.mtx`	5.0	3072	119808	0.20265
`conf5.0-00l4x4-2200.mtx`	5.0	3072	119808	0.20235
`conf5.0-00l4x4-2600.mtx`	5.0	3072	119808	0.21070
`conf6.0-00l4x4-2000.mtx`	6.0	3072	119808	0.15968
`conf6.0-00l4x4-3000.mtx`	6.0	3072	119808	0.16453
`conf5.4-00l8x8-0500.mtx`	5.4	49152	1916928	0.17865
`conf5.4-00l8x8-1000.mtx`	5.4	49152	1916928	0.17843
`conf5.4-00l8x8-1500.mtx`	5.4	49152	1916928	0.17689
`conf5.4-00l8x8-2000.mtx`	5.4	49152	1916928	0.17835
`conf6.0-00l8x8-2000.mtx`	6.0	49152	1916928	0.15717
`conf6.0-00l8x8-3000.mtx`	6.0	49152	1916928	0.15649
`conf6.0-00l8x8-8000.mtx`	6.0	49152	1916928	0.15623

References. A survey of lattice gauge theory is given in

M. Creutz: Quarks, Gluons, and Lattices, Cambridge University Press, (1986)
I. Montvay and G. Munster: Quantum Fields on the Lattice, Cambridge University Press (1994)

More background information can be found at various locations on the Web. Search for "High Energy Physics" (HEP). A list of HEP Web sites is available at CERN (European Laboratory for Particle Physics).

A PostScript version of this information is also available.

Matrices in this set:

conf5.0-00l4x4-1000 (complex unsymmetric, 3072 by 3072, 119808 entries), Quantum chromodynamics, b=5.0, k_c=0.20611
conf5.0-00l4x4-1400 (complex unsymmetric, 3072 by 3072, 119808 entries), Quantum chromodynamics, b=5.0, k_c=0.20328
conf5.0-00l4x4-1800 (complex unsymmetric, 3072 by 3072, 119808 entries), Quantum chromodynamics, b=5.0, k_c=0.20265
conf5.0-00l4x4-2200 (complex unsymmetric, 3072 by 3072, 119808 entries), Quantum chromodynamics, b=5.0, k_c=0.20235
conf5.0-00l4x4-2600 (complex unsymmetric, 3072 by 3072, 119808 entries), Quantum chromodynamics, b=5.0, k_c=0.21070
conf6.0-00l4x4-2000 (complex unsymmetric, 3072 by 3072, 119808 entries), Quantum chromodynamics, b=6.0, k_c=0.15968
conf6.0-00l4x4-3000 (complex unsymmetric, 3072 by 3072, 119808 entries), Quantum chromodynamics, b=6.0, k_c=0.16453
conf5.4-00l8x8-0500 (complex unsymmetric, 49152 by 49152, 1916928 entries), Quantum chromodynamics, b=5.4, k_c=0.17865
conf5.4-00l8x8-1000 (complex unsymmetric, 49152 by 49152, 1916928 entries), Quantum chromodynamics, b=5.4, k_c=0.17843
conf5.4-00l8x8-1500 (complex unsymmetric, 49152 by 49152, 1916928 entries), Quantum chromodynamics, b=5.4, k_c=0.17689
conf5.4-00l8x8-2000 (complex unsymmetric, 49152 by 49152, 1916928 entries), Quantum chromodynamics, b=5.4, k_c=0.17835
conf6.0-00l8x8-2000 (complex unsymmetric, 49152 by 49152, 1916928 entries), Quantum chromodynamics, b=6.0, k_c=0.15717
conf6.0-00l8x8-3000 (complex unsymmetric, 49152 by 49152, 1916928 entries), Quantum chromodynamics, b=6.0, k_c=0.15649
conf6.0-00l8x8-8000 (complex unsymmetric, 49152 by 49152, 1916928 entries), Quantum chromodynamics, b=6.0, k_c=0.15623

The Matrix Market is a service of the Mathematical and Computational Sciences Division / Information Technology Laboratory / National Institute of Standards and Technology.

[ Home ] [ Search ] [ Browse ] [ Resources ]

Last change in this page: Wed Sep 22 13:34:27 US/Eastern 2004 [Comments: ]