Matrix Set TUBULAR

TUBULAR: Tubular Reactor Model

from the NEP Collection

Set TUBULAR
Source:	K. Meerbergen and D. Roose, Katholieke Universiteit Leuven, Belgium
Discipline:	Computational fluid dynamics

The conservation of reactant and energy in a homogeneous tube of length L in dimensionless form is modeled by

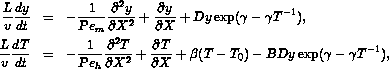
$L/v dy/dt= -1/P_{e_m}d^2y/dX^2 +dy/dX+D y exp(gamma-gamma T^(-1)); L/v dT/dt = -1/P_{e_h}d^T/dX^2 +dT/dX+beta(T-T_0)-bDy exp(gamma-gamma T^(-1))$

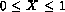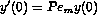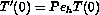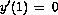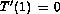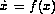where y and T represent concentration and temperature and 0<=X<=1 denotes the spatial coordinate. The boundary conditions are $y'(0)=P_{e_m} y(0)$ , $T'(0)=P_{e_h} T(0)$ , y'(1)=0 and T'(1)=0 . Central differences are used to discretize in space. For $X^T=[y_1,T_1,y_2,T_2,...y_{N/2},T_{N/2}]$ , the equations can be written as dot(x)=f(x) . The parameters in the differential equation are set to P_{e_m} = P_{e_h} = 5, B = 0.5, gamma = 25, beta = 3.5 and D = 0.2662. One seeks the rightmost eigenvalues of the Jacobian matrix 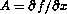A=df/dx . A is a banded matrix with bandwidth 5.

Matrices in this set:

TUB100 (real unsymmetric, 100 by 100, 396 entries)
TUB1000 (real unsymmetric, 1000 by 1000, 3996 entries)

The Matrix Market is a service of the Mathematical and Computational Sciences Division / Information Technology Laboratory / National Institute of Standards and Technology.

[ Home ] [ Search ] [ Browse ] [ Resources ]

Last change in this page: Wed Sep 22 13:37:28 US/Eastern 2004 [Comments: ]