

| Set ROBOTICS | |
|---|---|
| Source: | H. Ren, University of California, Berkeley |
| Discipline: | Robotic control |
The Stewart platform, also called left hand, is a parallel manipulator with six prismatic joints connecting two rigid bodies, or platforms. The base platform is considered fixed while the top platform, or end-effector, is moving in 3-dimensional space, controlled by the lengths of joints. Parallel robots are especially useful when high stiffness and position precision are predominant requirements. The platform has one degree of freedom per joint; the position and orientation of the top platform is specified by six parameters, namely three for the orientation and three for the position in 3D space. The forward kinematics assumes that the leg lengths are known and the displacement of the top platform is to be found. The algebraic problem reduces to the solution of a well-constrained system of polynomial equations. By using (sparse) resultant method, solving the system of polynomial equations reduces to solving the generalized eigenproblem 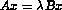 . The computational task is to compute the real eigenvalues and the corresponding eigenvectors (most of the eigenvalues are complex). Though the given model problem is of order 480, eigenvalue problems with thousands of unknowns commonly arise in this field.
. The computational task is to compute the real eigenvalues and the corresponding eigenvectors (most of the eigenvalues are complex). Though the given model problem is of order 480, eigenvalue problems with thousands of unknowns commonly arise in this field.
It is requested to compute the real eigenvalues and the corresponding eigenvectors, although most of the eigenvalues are complex. It is desired to solve such matrix eigenvalue problem of order a few thousands.
![[rbs480a Icon]](rbs480a_tiny.gif) RBS480A (real unsymmetric, 480 by 480, 17088 entries)
RBS480A (real unsymmetric, 480 by 480, 17088 entries)
![[rbs480b Icon]](rbs480b_tiny.gif) RBS480B (real unsymmetric, 480 by 480, 17088 entries)
RBS480B (real unsymmetric, 480 by 480, 17088 entries)
[ Home ] [ Search ] [ Browse ] [ Resources ]
Last change in this page: Wed Sep 22 13:37:27 US/Eastern 2004 [Comments: ]