The Matrix Market

Home Search Browse Resources

MVMODE: Model Eigenvalue Problem of ODEs

from the NEP Collection

Matrix Generator MVMODE
Source: G.W. Stewart, University of Maryland
Discipline: Ordinary differential equations
Language: Fortran
Output format: matrix-vector multiply

Consider the following eigenvalue problem of an ordinary differential equation

y''+mu^2 y=0

with the boundary conditions

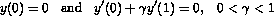y(0)=0 and y'(0)+gamma y'(1)=0 for 0<gamma<1.

It can be shown that the eigenvalues mu are given by

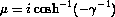mu=i arccosh(-gamma^(-1)),

which are complex. The solutions of this equation are of the form

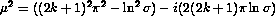
mu^2=((2k+1)^2 pi^2 - ln^2(sigma)-i(2(2k+1)pi ln(sigma))

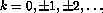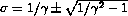for k=0,+/-1,+/-2,..., where sigma=1/gamma +/1 sqrt(1/gamma^1-2).

The eigenproblem of (3) can be approximated by finite differences as follows. Let yi denote the approximate solution at the point 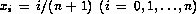x_i=i/(n+1) for i=0,1...n. Replacing the second derivatives in (3) with a centered difference operators to obtain the generalized matrix eigenvalue problem

A y = -mu^2 B y,

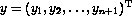for y=(y_1,y_2,...y_{n+1})^T", where with 1's on off-diagonals, -2 on diagonal, and an additional row appended with values (4,-1,... gamma, -4gamma, 3gamma)" >

and 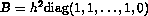B=h^2 diag(1,1,...1,0). Problem (4) can be recast as the standard eigenvalue problem

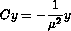C y= - 1/mu^2 y,

where 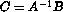C=A^(-1) B.

The matrix-vector products Y = CX can be formed by solving the linear system AY = BX for Y using the banded Gaussian elimination. Fortran calling sequence for Y = CX.

In the data files, 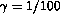gamma=1/100.

Parameters:

Nthe order of the matrix
GAMMAboundary condition parameter

Links:

Matrix Instances:

The Matrix Market is a service of the Mathematical and Computational Sciences Division / Information Technology Laboratory / National Institute of Standards and Technology.

[ Home ] [ Search ] [ Browse ] [ Resources ]

Last change in this page: Wed Sep 22 13:37:31 US/Eastern 2004 [Comments: ]