The Matrix Market

Home Search Browse Resources

MVMMCD: Model 2-D Convection Diffusion Operator

from the NEP Collection

Matrix Generator MVMMCD
Source: unclear
Discipline: Computational fluid dynamics
Language: Fortran
Output format: matrix-vector multiply

This test matrix is from the following constant-coefficient convection diffusion equation which is widely used for testing and analyzing numerical methods for the solution of linear system of equations,

-Delta u + 2p_1 u_x + 2p_2 u_y - p_3 u = f in [0,1]^2; u = g on partial[0,1]^2

where p1, p2 and p3 are positive constants. Discretization by the finite difference scheme with a 5-point stencil on a uniform m × m grid gives rise to a sparse linear system of equations

A u = b

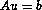
where A is of order m2 and u and b are now vectors of size m2. Centered differences are used for the first derivatives. If the grid points are numbered using the row-wise natural ordering, then A is a block tridiagonal matrix of the form

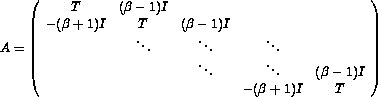Tridiagonal matrix with -(beta+1)I, T and (beta-1)I on the three diagonals,

with

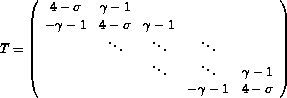Tridiagonal matrix with -gamma-1, 4-sigma and gamma-1 on the three diagonals,

where 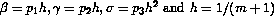beta=p_1 h; gamma=p_2 h; sigma=p_3 h^2 and h=1/(m+1).

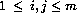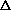The spectral decomposition of the convection diffusion matrix is known. For 1 <= i,j <= m, if Delta is a diagonal matrix with ((i-1)m+j)th diagonal entry

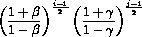((1+beta)/(1-beta))^((i-1)/2)*,

then 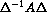Delta^(-1) A Delta is symmetric. For 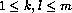1 <= k,l <=m, let (k,l) denote (k-1)m-l. Then the (k,l)th unnormalized eigenvector of 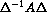Delta^(-1) A Delta has (i,j)th entry

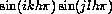sin(i k h pi) sin(j l h pi).

The reader may now verify that the (k,l)th eigenvalue of A is

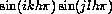sin(i k h pi) sin(j l h pi).

Figure 1 shows the eigenvalue distribution of 961 by 961 convection diffusion matrix with p1 = 25, p2 = 50 and p3 = 250.

Since the normalized eigenvectors of a symmetric matrix are orthogonal, the eigenvectors of A are graded like the diagonal of 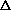Delta and the condition number of the eigenvalue problem for A is

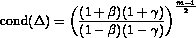cond(Delta)=(((1+beta)(1+gamma)) /((1-beta)(1-gamma)))^((m-1)/2)>.</CENTER><P><P> We note that, in practice, the choice of the mesh size h and the coefficients p<SUB>1</SUB>, p<SUB>2</SUB> and p<SUB>3</SUB> have to satisfy certain conditions for the discretization to be stable. We refer the reader to the references for the discussion of this issue.<P> Elman and Streit tested preconditioners for linear systems on six convention-diffusion matrices arising on a 31 by 31 grid. Note that when p<SUB>1</SUB> and p<SUB>2</SUB> are large compared to the grid size, the local error in the discretization is significant. Also note that when p<SUB>1</SUB> and p<SUB>2</SUB> are large the solution, u, forms boundary layers which are not practical to resolve using regular grids.<P> The following is the FORTRAN calling sequence for forming matrix-vector AX or A<SUP>T</SUP>X: <A HREF=Fortran calling sequence.

Parameters:

Norder of the matrix (must be the square of an integer)
p1coefficient of 2ux in differential operator
p2coefficient of 2uy in differential operator
p3coefficient of -u in differential operator

Links:

Matrix Instances:

The Matrix Market is a service of the Mathematical and Computational Sciences Division / Information Technology Laboratory / National Institute of Standards and Technology.

[ Home ] [ Search ] [ Browse ] [ Resources ]

Last change in this page: Wed Sep 22 13:37:31 US/Eastern 2004 [Comments: ]