

| Matrix Generator MVMBWM | |
|---|---|
| Source: | Y. Saad, University of Minnesota |
| Discipline: | Chemical engineering |
| Language: | Fortran |
| Output format: | matrix-vector multiply |
This problem models the concentration waves for reaction and transport interaction of chemical solutions in a tubular reactor. The concentrations x(t,z) and y(t,z) of two reacting and diffusing components are modeled by the system
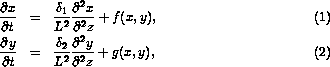
with the initial conditions 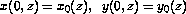 , and the Dirichlet boundary conditions
, and the Dirichlet boundary conditions 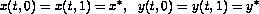 , where
, where 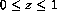 is the space coordinate along the tube, and t is time. Raschman et al. considered in particular the so-called Brusselator wave model in which
is the space coordinate along the tube, and t is time. Raschman et al. considered in particular the so-called Brusselator wave model in which
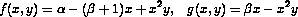
. Then, the above system admits the trivial stationary solution 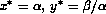 . In this problem one is primarily interested in the existence of stable periodic solutions to the system as the bifurcation parameter L varies. This occurs when the eigenvalues of largest real parts of the Jacobian of the right hand side of (1) and (2) are evaluated at the steady station solution, is purely imaginary. For the purpose of verifying this fact numerically, one first needs to discretize the equations with respect to the variable z and compute the eigenvalues with largest real parts of the resulting discrete Jacobian.
. In this problem one is primarily interested in the existence of stable periodic solutions to the system as the bifurcation parameter L varies. This occurs when the eigenvalues of largest real parts of the Jacobian of the right hand side of (1) and (2) are evaluated at the steady station solution, is purely imaginary. For the purpose of verifying this fact numerically, one first needs to discretize the equations with respect to the variable z and compute the eigenvalues with largest real parts of the resulting discrete Jacobian.
If we discretize the interval [0,1] using n interior points with the mesh size 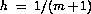 , then the discretized Jacobian of the system is a 2x2 block matrix of the form
, then the discretized Jacobian of the system is a 2x2 block matrix of the form
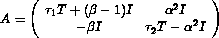 ,
, where T = tridiag{1,-2,1}, 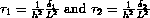 .
.
The exact eigenvalues of J are known since there exists a quadratic relation between the eigenvalues of the matrix A and those of the classical difference matrix T = tridiag{1,-2,1}. The following segment is the Matlab M-file for computing the 2m eigenvalues of A: mvmbwm M-file segment.
Figure 1 shows the 32 rightmost eigenvalue distribution of 200 by 200 of the matrix A (m=100) corresponding to the set of parameters
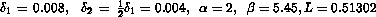
as used in Saad's book.
The following is the FORTRAN calling sequence for forming matrix-vector AX or ATX: Fortran calling sequence. In addition, the parameters 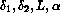 and
and 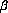 are set as internal parameters.
are set as internal parameters.
Parameters:
| N | order of the matrix (2m) |
| ALPHA | constant in reaction term for x |
| BETA | coefficient in reaction term for y |
| DELT1 | diffusion coefficient for x |
| DELT2 | diffusion coefficient for y |
| L | bifurcation parameter (L2 divides DELT1 and DELT2) |
![[bwm200 Icon]](bwm200_tiny.gif) BWM200 (real unsymmetric, 200 by 200, 796 nonzeros) Parameters: N=200, DELT1=0.008, DELT2=0.004, L=0.51302, ALPHA=2, BETA=5.45 ?
BWM200 (real unsymmetric, 200 by 200, 796 nonzeros) Parameters: N=200, DELT1=0.008, DELT2=0.004, L=0.51302, ALPHA=2, BETA=5.45 ?
![[bwm2000 Icon]](bwm2000_tiny.gif) BWM2000 (real unsymmetric, 2000 by 2000, 7996 nonzeros) Parameters: N=2000, DELT1=0.008, DELT2=0.004, L=0.51302, ALPHA=2, BETA=5.45 ?
BWM2000 (real unsymmetric, 2000 by 2000, 7996 nonzeros) Parameters: N=2000, DELT1=0.008, DELT2=0.004, L=0.51302, ALPHA=2, BETA=5.45 ?
[ Home ] [ Search ] [ Browse ] [ Resources ]
Last change in this page: Wed Sep 22 13:37:30 US/Eastern 2004 [Comments: ]