Matrix Set GEDNEY

GEDNEY: Dispersive Waveguide Structures

from the NEP Collection

Set GEDNEY
Source:	S. Gedney and U.D. Navsariwala, University of Kentucky
Discipline:	Electrical engineering

This is a complex symmetric eigenvalue problem 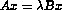A x = lambda B x , where both A and B are complex and symmetric, but not Hermitian. Moreover, the matrices A and B are of the forms

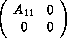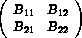$Matrix((A_{1,1},0),(0,0))$ and $Matrix((B_{1,1},B_{1,2}), (B_{2,1},B_{2,2}))$ ,

respectively. In the work of Tan and Pan, it is shown that the eigenvalue problem is derived from using the edge element method to solve the waveguide problem of conductors with finite conductivity and cross section in a lossy dielectric medium. The matrix size can easily reach a few thousands.

Matrices in this set come in pairs, corresponding to the matrices in the generalized eigenproblem Ax = (lamba)Bx. The matrices are named DWGnnnnA and CWGnnnnB, respectively.

The subblock matrix A₁₁ is 705 by 705, and banded. The computational task is to find the eigenvalues with the smallest positive real parts.

Matrices in this set:

DWG961A (complex symmetric indefinite, 961 by 961, 3405 entries)
DWG961B (complex symmetric indefinite, 961 by 961, 10591 entries)

The Matrix Market is a service of the Mathematical and Computational Sciences Division / Information Technology Laboratory / National Institute of Standards and Technology.

[ Home ] [ Search ] [ Browse ] [ Resources ]

Last change in this page: Wed Sep 22 13:37:25 US/Eastern 2004 [Comments: ]