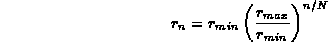
Suitable choice of a radial grid is key to obtaining accurate numerical solutions of the integro-differential equations of density-functional theory. The codes in our test suite make different choices for the radial grid. Two codes make perhaps the simplest choice, an exponentially increasing grid
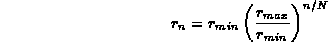
with three parameters: the minimum radius,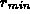 
,
the maximum radius, 
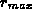, and the number of intervals, N.
The application of the exponential
grid to the atomic Schrödinger equation has been discussed
by Desclaux[8].
For one code we used N = 15788,
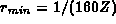, and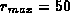 
.
(All distances are in atomic units.)
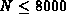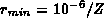Another code used 
, 
,
and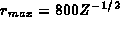 
; in this case, the energies were
extrapolated to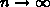 
using an 
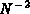or
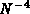dependence, depending on the quantity in question.
Another code chooses a grid which is nearly linear near the origin, and exponentially increasing at large r,
which again is determined by three parameters, a, b, and N.
This grid includes the origin explicitly as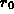 
.
In this case, we took 
, 
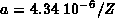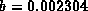, and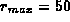 
,
leading to N = 7058 for H, increasing to N = 9021 for U,
and to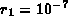 
for H, decreasing to 
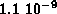for U.
A fourth code uses a change of variable technique:
A uniform grid is taken in the transformed variable from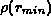 
to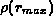 
where the parameters are taken to be
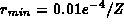, for atomic number Z, and 
.
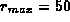The number of points increased from N = 2113 for H to
N = 2837 for U.
The density of points chosen in the latter two codes - linear near the
origin and exponentially increasing at large r -
is similar to that suggested from theoretical considerations[9].