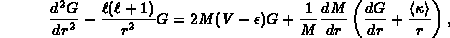
The inclusion of relativistic effects doubles the number of degrees of freedom in atomic calculations. However, sometimes it is desirable to include some of the effects of relativity without increasing the number of degrees of freedom. Specifically, it is possible to neglect the spin-orbit splitting while including other relativistic effects, such as the mass-velocity term, the Darwin shift, and (approximately) the contribution of the minor component to the charge density.
Koelling and Harmon[14] have proposed a method to achieve this end, which we call the scalar relativistic local density approximation (ScRLDA). (Sc is used to avoid confusion with spin-polarization which is abbreviated S.) This is a simplified version of the RLDA. The equations to solve are:
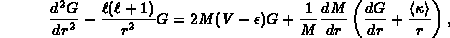
where 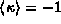 is the degeneracy-weighted average value
of the Dirac's
is the degeneracy-weighted average value
of the Dirac's  for the two spin-orbit-split levels, and
for the two spin-orbit-split levels, and  is the eigenvalue in Hartrees, with the same
meaning as in the RLDA.
is the eigenvalue in Hartrees, with the same
meaning as in the RLDA.
The parameter M is given by

where  is the fine structure constant.
The charge density is related to G by the usual non-relativistic formula,
is the fine structure constant.
The charge density is related to G by the usual non-relativistic formula,

without an explicit contribution from the minor component 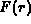 .
.